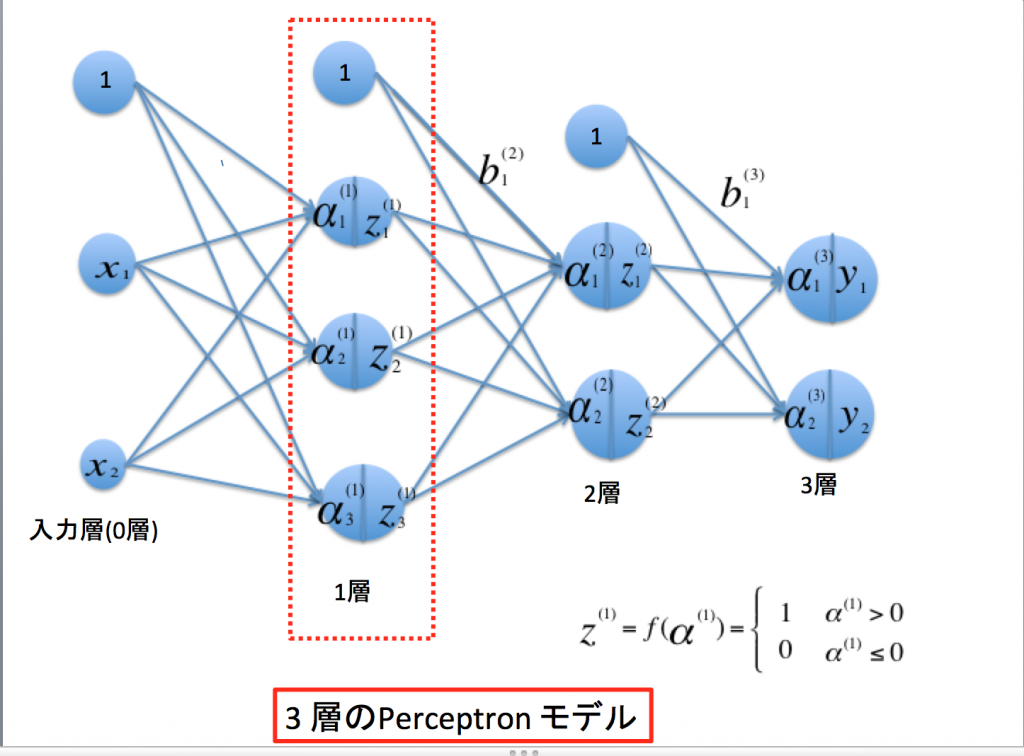
Fig.1 　3層で構成されるニューラル・ネットワークの関係

Fig.2. 第１層のneuronへの入力総和の行列表示。

(1) 第１層への入力と第１層からの出力

Fig.1とFig.2で求められる第1層に入力される重み付き総和をpythonで実装する。ここで、第0層の出力信号、重み、閾値は適当な値を設定していることに注意。

import numpy as np

X = np.array([1.0,0.5])               # 第0層の出力

W１ =np.array([[0.1,0.3,0.5],　# 第１層への重み

[0.2,0.4,0.6]])

B１ = np.array([0.1,0.2,0.3])　# 第１層への閾値

A１=np.dot(X, W１) + B１　　　# 第１層への入力

print(‘第0層の出力:’, X);

print(‘第１層への入力:’,A１)

[OutPut]

第0層の出力:[1.      0.5 ]

第１層への入力:[0.3   0.7   1.1 ]

また、第１層からの出力信号はsigmoid関数の引数として、A1を代入すれば、Z１ =(z1, z2, z3) が計算できる。

def sigmoid(x):

return 1/(1 + np.exp(-x))

Z１ = sigmoid(A１)

print(‘第１層からの出力:’,Z1)

[OutPut]

第１層からの出力: [0.57444252  0.66818777 0.75026011]

(2) 第２層への入力と第２層からの出力

第２層への入力と出力のpythonコードは次の様になる。

Z１が第２層への入力になっている以外は第１層の時と同じである。

W２= np.array([[0.1,0.5],

[0.2, 0.7],

[0.3, 0.9]])

B２= np.array([0.1,0.2])

A２= np.dot(Z１,W２) + B２

Z２= sigmoid(A２)

print(‘第２層の入力:’, A２)

print(‘第２層の出力:’, Z２)

[OutPut]

第２層の入力: [0.51615984  1.63018679]

第２層の出力: [0.62624937  0.83619523]

(3) 第3層への入力と第3層からの出力

第３層への入力と出力をpythonで実装する。第３層への入力はこれまでと同様であるが、第３層の活性化関数として入力をそままま出力する恒等関数ほ使う。

def  identf(x):

return x

W３= np.array([[0.1, 0.3],

[0.2, 0.4]])

B３= np.array([0.1, 0.2])

A３= np.dot(Z２, W３) + B３

Y = identf(A３)

print(‘第３層への入力:’, A３)

print(‘第３層への出力:’, Y)

[OutPut]

第３層への入力: [0.32986398  0.80597242]

第３層への出力:　[0.32986398, 0.80597242]

(4) ３層のNeural networkのpythonでの実装

import numpy as np

# シグモイド関数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))    

# 恒等関数
def identity(x):
    return x

# ニューラルネットワークの初期化を行う関数
def create_network():
    network = {}                                # ディクショナリを作成
    network['w1'] = np.array([[0.1, 0.3, 0.5],  # 第1層への重み
                              [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])   # 第1層へのバイアス
    network['w2'] = np.array([[0.1, 0.5],       # 第2層への重み
                              [0.2, 0.7],
                              [0.3, 0.9]])
    network['b2'] = np.array([0.1, 0.2])        # 第2層へのバイアス
    network['w3'] = np.array([[0.1, 0.3],       # 第3層への重み
                              [0.2, 0.5]])
    network['b3'] = np.array([0.1, 0.2])        # 第3層へのバイアス

    return network                              # 重み、バイアスを返す
# 各層への伝達を実行する関数
def propagation(network,          # ニューラルネットワークの重み、バイアス
            x                 # 第0層の出力値
           ):
    # 各層への重みを変数に格納
    w1, w2, w3 = network['w1'], network['w2'], network['w3']
    # 各層へのバイアスを変数に格納
        w1, w2, w3 = network['w1'], network['w2'], network['w3']
    # 各層へのバイアスを変数に格納
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1   # 第1層の入力
    z1 = sigmoid(a1)          # 第1層の出力(シグモイド関数)
    a2 = np.dot(z1, w2) + b2  # 第2層の入力
    z2 = sigmoid(a2)          # 第2層の出力(シグモイド関数)
    a3 = np.dot(z2, w3) + b3  # 第3層の入力
    y = identity(a3)          # 第3層の出力(恒等関数)

    return y                  # 第3層の出力値を返す

# 実行ブロック #
network = create_network()# ニューラルネットワークの初期化
x = np.array([1.0, 0.5]) # 第0層の出力値を設定
y = propagation(network, x) # ニューラルネットワークの各層の伝達を実行
print(y) # 第3層の出力値を表示
=====================================
[OutPut]
[0.32986398 0.80597242]　# 第3層の出力値を表示

参考文献:

夢見るディープラーニング: ニューラルネットワーク[Python実装]入門,

第2章、金城悛哉、秀和システム、2018.